Practice room for MathJax

This wiki is equipped with MathJax: http://www.pmwiki.org/wiki/Cookbook/MathJax

There's a handy online Latex editor, with which you can create Latex math, which is basically what is supported by LaTeXMathML...

 Everything you put in between  {$  and $} gets interpreted as Latex math.

Feel free to play around below to see how this works:

This is an inline {$ \delta $} test.

$W_{11} = m c^2 = m \frac{l^2}{t^2} $

$$ \int _a ^b f^{\prime}(x)\, dx = f(b) - f(a) $$

$$R_x = 10.0 \times \sin(R_\phi)$$

$$\sum_{n=1}^\infty \frac{1}{2^n}$$

$\lim_{x\to\infty} f(x) = k \choose r + \frac ab \sum_{n=1}^\infty a_n + \displaystyle{ \left\{ \frac{1}{13} \sum_{n=1}^\infty b_n \right\} }$

$$\$\alpha + \$\beta = \$(\alpha + \beta)$$

$$\begin{eqnarray} x & = & \frac{-7 \pm \sqrt{49 - 24}}{6} \\ & = & -2 \textrm{ or } -\frac13. \end{eqnarray}$$

$$\displaystyle{ V_i = C_0 - C_3 \frac{C_1\cos(\theta_i+C_3)}{C_4+C_1\cos(\theta_i+C_2)} }$$

Some Greek letters:

See here for more examples of letters, etc.

\phi	$ \phi $
\varphi	$ \varphi $
\psi	$ \psi $
\Omega	$ \Omega $
\Gamma	$ \Gamma$
\Delta	$ \Delta $
\eta	$ \eta $
\epsilon	$ \epsilon $
\theta	$ \theta $

ASCIIMath

Some more examples at: http://www1.chapman.edu/~jipsen/mathml/asciimath.html

Example: Solving the quadratic equation. Finally we move {$ b/(2a) $} to the right and simplify to get the two solutions: {$ %num=5% x_(1,2)=(-b+-sqrt(b^2-4ac))/(2a) $}

some actal forrmulas from Dollard:

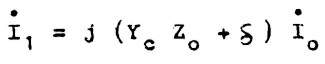
In LatexMath:

$$ \dot I_1 = j ( Y_c Z_0 + \delta) \dot I_0 $$

(13)

Bigger fonts:

$ \dot I_1 = j ( Y_c Z_0 + \delta) \dot I_0 $	(13)
$ \dot I_1 = j ( Y_c Z_0 + \delta) \dot I_0 $	(13)
$ \dot I_1 = j ( Y_c Z_0 + \delta) \dot I_0 $	(13)

In ASCIIMath:

{$ %num% dotI_1 = j (Y_c Z_0 + delta) dotI_0 $}

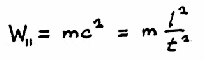
In ASCIIMath:

{$ W_1 = frac{varphi}{t} $}

Lines per second (Volts)

In LatexMath:

$ W_1 = \frac {\varphi} {t} $

Lines per second (Volts)

some further formulas from Dollard in LatexMath:

$ I = \frac {\psi} {t} $

Lines per second (Amperes)

$\begin{eqnarray} x & = & \frac{-7 \pm \sqrt{49 - 24}}{6} \\ & = & -2 \textrm{ or } -\frac13. \end{eqnarray}$

$\begin{eqnarray} V_0 & = & \frac{1}{\sqrt {L_0 C_0}} \\ & = & \eta V_c \end{eqnarray}$

Units/sec (5)

$\begin{eqnarray} V_0 & = & \eta V_c \\ & = & \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array}^2 \end{eqnarray}$

Units/sec (5)

$\begin{eqnarray} V_0 & = & \eta V_c \\ & = & \left[ \begin{array}{cc} \frac{1.77}{p} + \frac{3.94}{p}n \end{array} \right]^\frac12 \end{eqnarray}$

$2 \pi 10^9$ Inch/sec (7)

$ V_c = \frac{1}{\sqrt {\mu \epsilon}} $

Units/sec (5)

$ \left( \theta \right) =\left[ \begin{array}{cc} \cos \left( \theta \right) & -\sin \left( \theta \right) \\ \sin \left( \theta \right) & \cos \left( \theta \right) \end{array} \right] $

$ F_0 = \frac{V_0}{ (l_0 . 4) } $

Cycles/sec (8)

$ Z_c = \sqrt {\frac{L_0}{C_0}}$

Ohms (9)

$ Z_s = \left[ \begin{array}{cc} (182.9 + 406.4n)p \end{array} \right]^\frac12 $

$ \frac{\pi}{2} 10^3$ Ohms (inches) (11)

$ u = \frac{R_0}{2 L_0} = ( \frac{2.72}{r}+ \frac{2.13}{l}) \pi \sqrt{F_0} $

Nepers/sec (inches) (12)

$$ \begin{eqnarray} 10xy^2+15x^2y-5xy & = & 5\left(2xy^2+3x^2y-xy\right) \\ & = & 5x\left(2y^2+3xy-y\right) \\ & = & 5xy\left(2y+3x-1\right) \end{eqnarray} $$

$ \begin{eqnarray} 10xy^2+15x^2y-5xy & = & 5\left(2xy^2+3x^2y-xy\right) \\ & = & 5x\left(2y^2+3xy-y\right) \\ & = & 5xy\left(2y+3x-1\right) \end{eqnarray} $

(10)

$ \begin{eqnarray} \phi_1 & = & \phi_0 cos \theta \\ \phi_{11} & = & \phi_0 sin \theta \\ \end{eqnarray} $

$\Bigg \rbrace$ (4)

$\begin{eqnarray} W & = & m c^2 \\ & = & \begin{array}{cc} m \frac{l^2}{t^2}\end{array} \end{eqnarray}$

Watt . sec (6)

$ \begin{eqnarray} \varphi & = & \frac{i}{W} \\ & = & \frac{l^2}{t} \frac{m}{\psi} \\ \end{eqnarray} $

$ \begin{eqnarray} & & lines (7)\\ & & (8)\\ \end{eqnarray}$

$ \varphi $	$ = \frac{i}{W} $	lines (7)
	$ = \frac{l^2}{t} \frac{m}{\psi} $	(8)

$\begin{eqnarray} \psi_11 & = & m c^2 T \\ & = & \begin{array}{cc} m \frac{l^2}{t^2}\end{array} \end{eqnarray}$

Watt . sec˛ (6)

$ \phi_{11} $	$ = m c^2 T $	Watt . sec˛
	$ = m \frac{l^2}{t} $	(9)